Offene Aufgaben

Offene Aufgaben

Unter Aufgaben versteht man die Aufforderung zum Lern-Handeln. Diese Handlungen können Aufforderung zum Begründen, Realisieren, Interpretieren, Identifizieren, Beurteilen, Systematisieren, Verknüpfen, Suchen, Erkennen, Beschreiben von mathematischen Begriffen, Werkzeugen, Zusammenhängen und Verfahren sein. Man unterscheidet dabei:

Nachfolgendes Video verdeutlicht die Ausführungen

PowerPoint-Foien zum Thema

Das nachfolgende Video thematisiert das Thema Blütenaufgaben

Hier noch ein Video zum Thema Fermi-Aufgaben

Aufgaben öffnen mit der Aufgabendrehscheibe

„Berechne das Volumen V eines Quaders mit den Kantenlängen a = 25cm, b = 48cm , c = 15cm !“ – ein typisches Beispiel für eine sogenannte geschlossene Aufgabe, wie sie sich (immer noch) zu Hauf in den Schulbüchern finden. Die SuS kennen (hoffentlich) die passende Formel (steht meistens als Überschrift über der Aufgabe), setzen ein und erhalten ein Ergebnis.

Solche Aufgaben können häufig mit wenig Aufwand geöffnet werden:

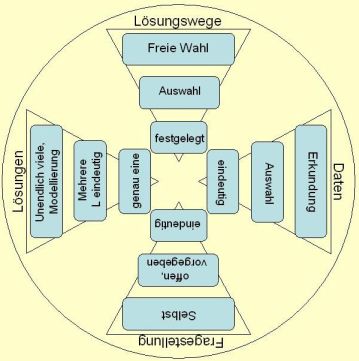
Eine Aufgabe ist eine geistige Anforderung an ein Individuum, bei der ein Anfangszustand (Fragestellung und gegebene Daten, z.B. die gegebenen Maße eines Quaders) vermöge einer gewissen Transformation (Lösungsweg, z.B. Volumenformel für einen Quader) in einen erwünschten Zielzustand (Lösung, z.B. Angabe des Volumens) zu überführen ist. Demnach gibt es drei Stellen, an denen die Offenheit beeinflusst werden kann. Michael Katzenbach (mathematik lehren, Heft 138, Oktober 2006, Seite 63-64) hat dies übersichtlich als Aufgabendrehscheibe dargestellt.

Beispiele finden Sie hier: https://die-mueden.de/html/kultur/k4-lebensbezug-aufgabenoeffnen.html

Literatur:

• Bruder, Leuders, Büchter: Mathematikunterricht entwickeln. Cornelsen Verlag.Bruder, Leuders, Büchter: Mathematikunterricht entwickeln. Cornelsen Verlag.